Эпичное тестовое задание на собеседовании…Прошу помочь с решением…

Евгений Равич пишет:
Знает ли спелеолог про 2/5/7, и может ли он помечать маршруты? Нужно делать допущения. Допустим, что может.

Что такое "в среднем" - не расшифровано.

Например, для первого варианта до выхода на свободу нужно пройти (с учетом  обязательного отрезка в 2 часа): 2, 7, 9 или 14 часов. Никакого среднего тут нет. Или/или.

Минимальное время - 2 часа, максимальное - 14. Надеюсь, еды и воды хватит.

Минимальное 2 часа, а максимального нет, он может до бесконечности ходить кругами и никогда оттуда не выйти, просто вероятность этого практически нулевая.

Под средним понимается математическое ожидание времени выхода, то есть для каждой ситуации есть своя вероятность и свое время выхода. Вероятности умножаются на соответствющие времена и суммируются, на самом деле суммируется бесконечный ряд, геометрическая прогрессия со знаменателем меньше 1 (сходящийся ряд).

В принципе могу привести решение, там видно, что это за величина, но корректное описание потребует времени.

Тут наверное корректнее сформулировать задачу так, каково среднеожидаемое время выхода спелеолога из пищеры.

Михаил Лурье пишет:

Евгений Равич пишет:
Знает ли спелеолог про 2/5/7, и может ли он помечать маршруты? Нужно делать допущения. Допустим, что может.

Что такое "в среднем" - не расшифровано.

Например, для первого варианта до выхода на свободу нужно пройти (с учетом  обязательного отрезка в 2 часа): 2, 7, 9 или 14 часов. Никакого среднего тут нет. Или/или.

Минимальное время - 2 часа, максимальное - 14. Надеюсь, еды и воды хватит.

Минимальное 2 часа, а максимального нет, он может до бесконечности ходить кругами и никогда оттуда не выйти, просто вероятность этого практически нулевая.

Вероятность я пока вообще не обсуждаю. Допущение выше в моем комментарии - что спелеолог может пометить маршрут - то есть три попытки максимум.

Под средним понимается математическое ожидание времени выхода, то есть для каждой ситуации есть своя вероятность и свое время выхода. Вероятности умножаются на время и суммируются, на самом деле суммируется бесконечный ряд, геометрическая прогрессия со знаменателем меньше 1 (сходящийся ряд).

При допущении о пометках это дискретная функция с 4 значениями. Других нет, средние не имеют смысла - как и беседа о вероятности и мат.ожидании. 

Тут наверное корректнее сформулировать задачу так, каково среднеожидаемое время выхода спелеолога из пищеры.

Корректнее было бы сказать в условии, может ли спелеолог идти по одному пути дважды.

Евгений Равич пишет:
Корректнее было бы сказать в условии, может ли спелеолог идти по одному пути дважды.

Спелеолог в темноте не может нечего пометить и не может ориентироваться при выходе из пещеры кроме того в какую сторону двигаться, и по одному и тому же круговому пути может ходить любое число раз.

Вот рещение задачи:

Есть 3 равновероятных события по выходу из исходной точки.

Путь 1) ведет к свободе и занимает T1 часа.
Путь 2) приводит в исходную точку и занимает T2 часов.
Путь 3) приводит в исходную точку и занимает T3 часов.

Каждое событие имеет одинаковую вероятность 1/3.

Рассмотрим путь 2 и 3 как одно событие с вероятностью 2/3. Поскольку выбор путей 2 и 3 равновероятны, то время пути по одному кругу примем (T2+T3)/2

Среднеожидаемое время выхода из пещеры займет время пути 1 и среднеожидаемое время хождение по кругу.

Пусть P(n) вероятность того, что спелеолог при выходе из пещеры сделает ровно n кругов.

Пусть P(≥n) вероятность того, что спелеолог при выходе из пещеры сделает больше или равно n кругов.

Среднеожидаемое время хождение по кругу, то есть математическое ожидание, есть сумма вероятностей, умноженных на время прохождения кругов:

P(1)*1*(T2+T3)/2 + P(2)*2*(T2+T3)/2 + …  P(n)*n*(T2+T3)/2 + …. =

= (T2+T3)/2 * (P(1)*1 + P(2)*2 + …  P(n)*n + ….)

Заметим, что:

P(≥n) = P(n) + P(n+1) + ……

Таким образом, вероятность P(n) входит в n вероятностей P(≥1), …. , P(≥n)

Значит

P(1)*1 + P(2)*2 + …  P(n)*n + …. = P(≥1) + P(≥2). + … + P(≥n) + ....

Среднеожидаемое время хождение по кругу:

(T2+T3)/2 * (P(≥1) + P(≥2). + … + P(≥n) + …)

P(≥1) = (2/3)^1

P(≥2) = (2/3)^2

P(≥n) = (2/3)^n

P(≥1) + P(≥2). + … + P(≥n) + …= (2/3)^1 + (2/3)^2 + …. + (2/3)^n + … = (1-2/3)/(2/3-1) = 2

Среднеожидаемое время хождение по кругу:

(T2+T3)/2 * 2 = T2+T3

Значит среднеожидаемое время выхода из пещеры:

T1+T2+T3

PS. Извиняюсь, что не ответил сразу, патроны кончились, в смысле сделал уже 10 комментариев.

Михаил Лурье пишет:
PS. Извиняюсь, что не ответил сразу, патроны кончились, в смысле сделал уже 10 комментариев.

Боже, как это прекрасно!

Но я поступил проще -- написал имитационную модель и запустил её на 10 000 циклов несколько раз.
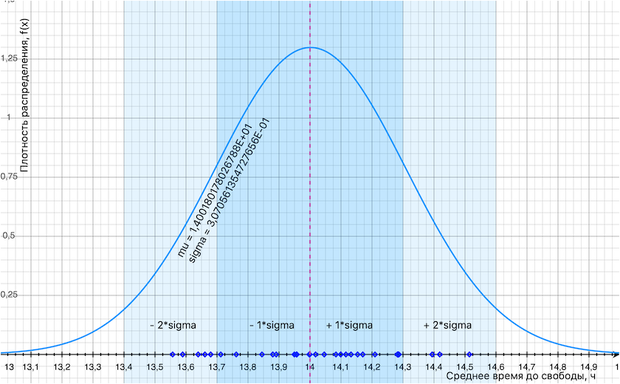
Собрал показатели, провел по ним функцию ошибок, дифференцировал её и нашел ответ -- это 14 часов среднее время до свободы.


65% всех попыток лягут в интервал 14 ±0,3 ч.
95% всех попыток лягут в интервал 14 ±0,6 ч.
Ну, и 99% окажутся в интервале 14 ±0,9 ч.

На всё это у меня ушло 10 минут :)

Кстати, обожаю количественные исследования, закон нормального распределения и функцию ошибок и вообще всякого рода сигмоиды :)

Кстати в логотипе Sennheiser именно она (функция ошибок):

Сергей Средний пишет:
Боже, как это прекрасно!Но я поступил проще -- написал имитационную модель и запустил её на 10 000 циклов несколько раз.Собрал показатели, провел по ним функцию ошибок, дифференцировал её и нашел ответ -- это 14 часов среднее время до свободы.

Все очень красиво!

Но если вернуться к теме дискуссии, на собеседование надо приходить со своими инструментами?

Михаил Лурье пишет:
Но если вернуться к теме дискуссии, на собеседование надо приходить со своими инструментами?

У меня всегда с собой ноутбук. Уже лет 25 как. Даже, когда я иду на пляж.

Михаил Лурье пишет:
Спелеолог в темноте не может нечего пометить и не может ориентироваться при выходе из пещеры кроме того в какую сторону двигаться, и по одному и тому же круговому пути может ходить любое число раз.

Вы сделали другие допущения, включая главное - у спелеолога бесконечный запас еды, воды и сил, он ест на ходу, не спит, а только ходит взад-вперед любое число раз. Ваше право.

Константин Комшуков пишет:
У меня другое отношение к трудоустройству и всему тому, что с этим связано.
Во-первых, я сразу принимаю за правило тот факт, что мне никто ничего не должен. Равно как и я никому не должен до момента получения офера и его акцептования с моей стороны.

Значит я не корректно выразился... Признаю свою ошибку. 

Во-вторых, у меня изначально нет оснований для того, чтобы сомневаться в чьей-то порядочности. Да, может потом сложиться по факту негативный опыт. Ну, ничего страшного, бывает. Сделал пометку в особой книжечке и дальше пошёл. В следующий раз уже на эти "грабли" не наступишь. Мог бы я проявлять особую бдительность, воспринимая все критически, для того, чтобы заранее снизить негативные последствия для себя ? Конечно. Но, одновременно, я бы этим самым сузил поле возможностей. Потому этим особо не заморачиваюсь. 

Да и не призывал я воспринимать всё с кртицизмом. Предлагал только порасуждать и не более - курсивом я их выделяю, а важное всегда жирным текстом. 

Евгений Равич пишет:
Вы сделали другие допущения, включая главное - у спелеолога бесконечный запас еды, воды и сил, он ест на ходу, не спит, а только ходит взад-вперед любое число раз. Ваше право.

Однажды сороконожку спросили как она управляет своими сорока ногами.
Сороконожка задумалась и больше не смогла ходить.

Сергей Средний пишет:

Евгений Равич пишет:
Вы сделали другие допущения, включая главное - у спелеолога бесконечный запас еды, воды и сил, он ест на ходу, не спит, а только ходит взад-вперед любое число раз. Ваше право.

Однажды сороконожку спросили как она управляет своими сорока ногами.
Сороконожка задумалась и больше не смогла ходить.

Не помните, кто спрашивал? Полагаю, что не Вы.

Интересное сравнение сороконожки со спелеологом, бесконечно гуляющим по коридорам. Примерно так же реалистично, как и беседы с насекомыми.

Евгений Равич пишет:
Михаил Лурье пишет: Спелеолог в темноте не может нечего пометить и не может ориентироваться при выходе из пещеры кроме того в какую сторону двигаться, и по одному и тому же круговому пути может ходить любое число раз.

Вы сделали другие допущения, включая главное - у спелеолога бесконечный запас еды, воды и сил, он ест на ходу, не спит, а только ходит взад-вперед любое число раз. Ваше право.

Ну это же математическая абстракция. Можно ее переформулировать, что это какая-то частица бегает по орбитам и у нее есть точка равновероятного перехода с орбиты на орбиту (точка бифуркации). Или спутник крутится по орбитам и проходит точку случайного измения орбиты.

Ну а если эту задачу рассмотреть в практической плоскости, то вероятность того, что спелеолог сделает больше или равно чем n кругов:

P(≥n) = (2/3)^n

Посмотрите как падает вероятность при росте n, так что скорее всего он уложится в какое-то приемлимое число кругов и приемлимое время выхода из пещеры.

Ну, можно, конечно, на собеседовании дать задачу про косцов, которую Лев Толстой в своей деревенской школе крестьянским детям задавал:

Артели косцов надо скосить два луга, один вдвое больше другого. Половину дня артель косила большой луг. После этого артель разделилась пополам, первая половина осталась на большом лугу и докосила его к вечеру до конца; вторая же половина косила малый луг, на котором к вечеру еще осталась часть луга, скошенного на другой день одним косцом за один день работы.

Сколько косцов было в артели?

Михаил Лурье пишет:

Евгений Равич пишет:
Михаил Лурье пишет: Спелеолог в темноте не может нечего пометить и не может ориентироваться при выходе из пещеры кроме того в какую сторону двигаться, и по одному и тому же круговому пути может ходить любое число раз.

Вы сделали другие допущения, включая главное - у спелеолога бесконечный запас еды, воды и сил, он ест на ходу, не спит, а только ходит взад-вперед любое число раз. Ваше право.

Ну это же математическая абстракция.

Абстракция - это хорошо, если в малых дозах. Поставим эксперимент и сравним результаты? Займет как раз 5-7 минут. Никакие формулы не нужны.

Можно ее переформулировать, что это какая-то частица бегает по орбитам и у нее есть точка равновероятного перехода с орбиты на орбиту (точка бифуркации). Или спутник крутится по орбитам и проходит точку случайного измения орбиты.

Нет, не стоит. Это совсем другая задача - частиц слишком много, и они, скорее всего, одинаковые. Теряем существенные для нас факторы.

Ну а если эту задачу рассмотреть в практической плоскости, то вероятность того, что спелеолог сделает больше или равно чем n кругов:

P(≥n) = (2/3)^n

Вероятности в быту лучше вообще не считать.
Они хороши для статфизики, идеальных монет и костей, но - главное - n --> 00. Не тот случай.

Предложение:

1) Возьмите 3 карты (2, 5 и 7), масти не важны.
2) Перетасуйте и посмотрите верхнюю. Запишите результат.
3) Если не 2 - положите обратно и повторите п.2, пока 2 не появится. Тасовать нужно тщательно! Это одна успешная серия.
4) И так 10 серий. Всё просто и наглядно.

Нет карт - отлично работает с тремя спичками.

Свою часть я сделал. 

Евгений Равич пишет:
Предложение: 1) Возьмите 3 карты (2, 5 и 7), масти не важны. 2) Перетасуйте и посмотрите верхнюю. Запишите результат.3) Если не 2 - положите обратно и повторите п.2, пока 2 не появится. Это серия.4) И так 10 серий. Всё просто и наглядно. Свою часть я сделал. 

Перетасуйте карты, запишите карту (2, 5, 7) и если не 2, то продолжайте.

После выпадения карты 2 просуммируйте записанные числа карт и оцените среднее ожидаемое значение.

Та же самая задача. По моему это называется орбита событий.

Михаил Лурье пишет:

Евгений Равич пишет:
Предложение: 1) Возьмите 3 карты (2, 5 и 7), масти не важны. 2) Перетасуйте и посмотрите верхнюю. Запишите результат.3) Если не 2 - положите обратно и повторите п.2, пока 2 не появится. Это серия.4) И так 10 серий. Всё просто и наглядно. Свою часть я сделал. 

Перетасуйте карты, запишите карту (2, 5, 7) и если не 2, то продолжайте.

После выпадения карты 2 просуммируйте записанные числа карт и оцените среднее ожидаемое значение.

Та же самая задача.

Совершенно верно - так эксперимент и планируется!

Но результат Вас, возможно, удивит. Эффект (непредсказуемость) малых выборок.

Евгений Равич -- явно не из этой сказки :)

Всегда удивляет -- одни берут и решают (делают), другие всем рассказывают почему решить (сделать) невозможно.
Наверное от СЛИШКОМ большого ума :)
"От многой мудрости многия скорби, и умножающий знание умножает печаль." -- Соломон.

Не так давно предложил здесь интересную задачу.
Есть данные о ежемесячной посещаемости портала E-xecutive -- суммарные посетители в месяц.
Спрогнозируйте число суммарных посетителей в августе, сентябре, октябре, ноябре, декабре, ...

А мы потом с учетом даты прогноза оценим ошибку и всё поймём.
Например так -- ошибка/дистанция для каждого прогноза -- так как чем больше дистанция, с которой делается прогноз, тем сложней попасть в яблочко.
Только пожалуйста не говорите, что это невозможно. Всё возможно. Только у одних ошибка (точнее критерий оценки) будет конским, а удругих как у хомячка.