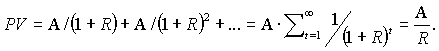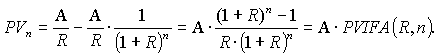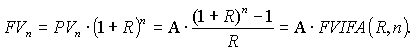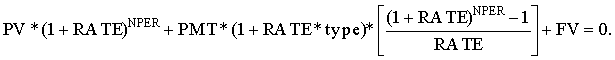Аннуитетные финансовые функции в Таблицах Google Docs — различия между версиями
(Новая страница: «leftНесмотря на то, что формула сложных процентов доступна пониманию учен...») |
|||
| Строка 1: | Строка 1: | ||
| − | [[Image: | + | [[Image:Tabl googl doks 1.jpg|left|Tabl googl doks 1.jpg]]Несмотря на то, что формула сложных процентов доступна пониманию ученика средней школы, усвоившего закон геометрической прогрессии, практика потребительского кредитования подтверждает необходимость дальнейшего укрепления финансовой грамотности заемщиков. <br> |
| − | Модель процентного роста и методы оценки потоков платежей давно запрограммированы на финансовых калькуляторах и в электронных таблицах как встроенные функции. <br> | + | Модель процентного роста и методы оценки потоков платежей давно запрограммированы на финансовых калькуляторах и в электронных таблицах как встроенные функции. <br> |
| − | Их имена: PV, FV, PMT стандартны - как SIN или COS для тригонометрии. <br> | + | Их имена: PV, FV, PMT стандартны - как SIN или COS для тригонометрии. <br> |
| − | С появлением электронных таблиц воплощено в жизнь наше интуитивное восприятие компьютера как большого калькулятора. Теперь эти программы есть и на смартфонах, так что мы можем отправляться в деловой поход, вооружившись портативным вычислительным устройством. <br> | + | С появлением электронных таблиц воплощено в жизнь наше интуитивное восприятие компьютера как большого калькулятора. Теперь эти программы есть и на смартфонах, так что мы можем отправляться в деловой поход, вооружившись портативным вычислительным устройством. <br> |
| − | Доступность Интернета и развитие распределенных облачных вычислений расширяет функционал наших маленьких компьютеров. <br> | + | Доступность Интернета и развитие распределенных облачных вычислений расширяет функционал наших маленьких компьютеров. <br> |
| − | Читателю предлагается элементарный справочный материал по аннуитетным расчетам с использованием финансовых функций облачного сервиса Таблицы Google Docs. <br> | + | Читателю предлагается элементарный справочный материал по аннуитетным расчетам с использованием финансовых функций облачного сервиса Таблицы Google Docs. <br> |
| − | Ранее было опубликовано пособие по технике финансовых вычислений на MS Excel, дающее ключ к применению стандартных финансовых функций, поспешно локализованных с кириллическими идентификаторами.<br> | + | Ранее было опубликовано пособие по технике финансовых вычислений на MS Excel, дающее ключ к применению стандартных финансовых функций, поспешно локализованных с кириллическими идентификаторами.<br> |
| − | <br> | + | <br> |
| − | == Определение аннуитета == | + | == Определение аннуитета == |
| − | Аннуитетом называется последовательность платежей одинакового размера, поступающих через равные промежутки времени (равномерная рента). Период времени между двумя соседними платежами является расчетным для начисления процентов за использование заемных средств. <br> | + | '''Аннуитетом''' называется последовательность платежей одинакового размера, поступающих через равные промежутки времени (равномерная рента). Период времени между двумя соседними платежами является расчетным для начисления процентов за использование заемных средств. <br> |
| − | [[Image:Tabl_googl_doks_2.jpg<br> | + | [[Image:Tabl_googl_doks_2.jpg]]<br> |
| − | ''Рис. 2. Тип аннуитета задает распределение платежей по границам процентных периодов.''<br> | + | ''Рис. 2. Тип аннуитета задает распределение платежей по границам процентных периодов.''<br> |
| − | <br> | + | <br> |
| − | Конечная последовательность платежей одинакового размера называется срочным аннуитетом. Срок n соответствует количеству платежей. В зависимости от момента поступления первого платежа различают два типа аннуитетов — пренумерандо (первый платеж поступает в начале первого периода) и постнумерандо (первый платеж поступает в конце первого периода). Аннуитет постнумерандо называют «обыкновенным».<br><br> | + | Конечная последовательность платежей одинакового размера называется срочным аннуитетом. Срок n соответствует количеству платежей. В зависимости от момента поступления первого платежа различают два типа аннуитетов — пренумерандо (первый платеж поступает в начале первого периода) и постнумерандо (первый платеж поступает в конце первого периода). Аннуитет постнумерандо называют «обыкновенным».<br><br> |
| − | == Будущая стоимость аннуитета == | + | == Будущая стоимость аннуитета == |
| − | Будущая стоимость (FV — англ. Future Value) равномерного потока платежей с учетом ставки процента за каждый период между платежами находится как сумма геометрической прогрессии <br> | + | Будущая стоимость (FV — англ. Future Value) равномерного потока платежей с учетом ставки процента за каждый период между платежами находится как сумма геометрической прогрессии <br> |
| − | [[Image: | + | [[Image:Tabl googl doks 3.jpg]]<br> |
| − | где A — член аннуитета (размер одного платежа), R — процентная ставка, n — число платежей (и число процентных периодов). | + | где A — член аннуитета (размер одного платежа), R — процентная ставка, n — число платежей (и число процентных периодов). |
| − | <u>Пример 1. </u>Согласно условиям договора, 5 платежей по 3 доллара регулярно приходят по схеме пренумерандо. Получатель аннуитета (кредитор) использует средства с доходностью R = 8% за период между платежами. Будущая стоимость одного платежа A=$3.00 через 1 расчетный период по ставке 8% составляет $3.00*1.08=$3.24. Через 2 периода по формуле сложных процентов $3.00*1.08*1.08=$3.24*1.08=$3.50. Какова будущая стоимость всего потока платежей в конце последнего периода? Детальный расчет будущей стоимости каждого платежа и всего аннуитета развернут на рис. 2. <br> | + | <u>Пример 1. </u>Согласно условиям договора, 5 платежей по 3 доллара регулярно приходят по схеме пренумерандо. Получатель аннуитета (кредитор) использует средства с доходностью R = 8% за период между платежами. Будущая стоимость одного платежа A=$3.00 через 1 расчетный период по ставке 8% составляет $3.00*1.08=$3.24. Через 2 периода по формуле сложных процентов $3.00*1.08*1.08=$3.24*1.08=$3.50. Какова будущая стоимость всего потока платежей в конце последнего периода? Детальный расчет будущей стоимости каждого платежа и всего аннуитета развернут на рис. 2. <br> |
| − | [[Image: | + | [[Image:Tabl googl doks 4.jpg]]<br> |
| − | ''<br>'' | + | ''<br>'' |
| − | ''Рис. 3. Вычисление будущей стоимости аннуитета по частям.'' | + | ''Рис. 3. Вычисление будущей стоимости аннуитета по частям.'' |
| − | Ответ: В условиях примера 1 поток платежей пренумерандо позволяет их получателю накопить сумму $19.01. В случае аннуитета постумерандо будущая стоимость достигает только $17.60 (все платежи «недорасли» бы еще один период).<br><br> | + | Ответ: В условиях примера 1 поток платежей пренумерандо позволяет их получателю накопить сумму $19.01. В случае аннуитета постумерандо будущая стоимость достигает только $17.60 (все платежи «недорасли» бы еще один период).<br><br> |
| − | == Современная стоимость аннуитета == | + | == Современная стоимость аннуитета == |
| − | <u>Пример 2</u>. Расчет современной (текущей, приведенной, дисконтированной) стоимости каждого из пяти периодических платежей и всего потока по ставке R=8% за период между платежами для аннуитета пренумерандо представлен в таблице на рис. 4 в варианте приведения дисконтирующими множителями к начальному моменту времени (отсчет ведется от 0), когда вносится первый платеж. | + | <u>Пример 2</u>. Расчет современной (текущей, приведенной, дисконтированной) стоимости каждого из пяти периодических платежей и всего потока по ставке R=8% за период между платежами для аннуитета пренумерандо представлен в таблице на рис. 4 в варианте приведения дисконтирующими множителями к начальному моменту времени (отсчет ведется от 0), когда вносится первый платеж. |
| − | Ответ: Текущая стоимость данного аннуитета равна $12.94. <br> | + | Ответ: Текущая стоимость данного аннуитета равна $12.94. <br> |
| − | [[Image: | + | [[Image:Tabl googl doks 5.jpg]]<br> |
| − | ''Рис. 4. Вычисление современной (текущей) стоимости аннуитета по частям.'' | + | ''Рис. 4. Вычисление современной (текущей) стоимости аннуитета по частям.'' |
| − | <br> | + | <br> |
| − | Современная стоимость (PV — англ. Present Value) срочного аннуитета (n < ∞) аналически оценивается как разница современных стоимостей двух бесконечных аннуитетов, моменты начала которых не совпадают. <br> | + | Современная стоимость (PV — англ. Present Value) срочного аннуитета (n < ∞) аналически оценивается как разница современных стоимостей двух бесконечных аннуитетов, моменты начала которых не совпадают. <br> |
| − | [[Image: | + | [[Image:Tabl googl doks 6.jpg]]<br> |
| − | Здесь использован результат из элементарной алгебры — современная стоимость бесконечного аннуитета PV (n = +∞) представляет собой сумму всех членов бесконечно убывающей геометрической прогрессии со знаменателем 1/(1+R), которая при R < –2 или R > 0 сходится к A/R: | + | Здесь использован результат из элементарной алгебры — современная стоимость бесконечного аннуитета PV (n = +∞) представляет собой сумму всех членов бесконечно убывающей геометрической прогрессии со знаменателем 1/(1+R), которая при R < –2 или R > 0 сходится к A/R: |
| − | Для вывода рабочей формулы современной стоимости срочного аннуитета из современной стоимости вечной ренты на момент времени 0 вычитается современная стоимость ее клона — вечной ренты, начинающейся на n периодов попозже. <br> | + | Для вывода рабочей формулы современной стоимости срочного аннуитета из современной стоимости вечной ренты на момент времени 0 вычитается современная стоимость ее клона — вечной ренты, начинающейся на n периодов попозже. <br> |
| − | [[Image: | + | [[Image:Tabl googl doks 7.jpg]]<br> |
| − | Вторая стоимость численно равна первой, но относится к моменту времени n, поэтому перед вычитанием ее необходимо дисконтировать по той же процентной ставке R на n расчетных периодов в прошлое. Эквивалентная будущая стоимость срочного аннуитета есть.<br> | + | Вторая стоимость численно равна первой, но относится к моменту времени n, поэтому перед вычитанием ее необходимо дисконтировать по той же процентной ставке R на n расчетных периодов в прошлое. Эквивалентная будущая стоимость срочного аннуитета есть.<br> |
| − | [[Image: | + | [[Image:Tabl googl doks 8.jpg]]<br> |
| − | В рассмотренном выше примере 1 верно $19.01=$12.94*1.08^5=$3.00*FVIFA(8%,5).<br><br> | + | В рассмотренном выше примере 1 верно $19.01=$12.94*1.08^5=$3.00*FVIFA(8%,5).<br><br> |
| − | == Процентные множители (финансовые коэффициенты в общепринятой нотации) == | + | == Процентные множители (финансовые коэффициенты в общепринятой нотации) == |
| − | FVIF(R,n) — англ. Future Value Interest Factor - процентный множитель будущей стоимости (коэффициент наращения). <br> | + | FVIF(R,n) — англ. Future Value Interest Factor - процентный множитель будущей стоимости (коэффициент наращения). <br> |
| − | [[Image: | + | [[Image:Tabl googl doks 9.jpg|center|Tabl googl doks 9.jpg]]<br> |
| − | FVIF(R,n) показывает, какую сумму можно нарастить из одной исходной денежной единицы благодаря регулярному присоединению сложных процентов по ставке R в течение n процентных периодов (срок наращения). | + | FVIF(R,n) показывает, какую сумму можно нарастить из одной исходной денежной единицы благодаря регулярному присоединению сложных процентов по ставке R в течение n процентных периодов (срок наращения). |
| − | PVIF(R,n) — англ. Present Value Interest Factor — процентный множитель современной стоимости (коэффициент приведения). <br> | + | PVIF(R,n) — англ. Present Value Interest Factor — процентный множитель современной стоимости (коэффициент приведения). <br> |
| − | [[Image: | + | [[Image:Tabl googl doks 10.jpg|center|Tabl googl doks 10.jpg]]PVIF(R,n) показывает, какую сумму достаточно было положить в банк на депозитный счет, чтобы в результате регулярного присоединения сложных процентов по ставке R в течение n процентных периодов получить ровно одну денежную единицу. |
| − | FVIFA(R,n) — англ. Future Value Interest Factor of Annuity — процентный множитель будущей стоимости (коэффициент наращения) аннуитета. <br> | + | FVIFA(R,n) — англ. Future Value Interest Factor of Annuity — процентный множитель будущей стоимости (коэффициент наращения) аннуитета. <br> |
| − | [[Image: | + | [[Image:Tabl googl doks 11.jpg|center|Tabl googl doks 11.jpg]]FVIFA(R,n) показывает, какую сумму можно накопить, постоянно получая выплаты единичного размера в течение срока n при регулярном начислении сложных процентов по ставке R за каждый период на уже аккумулированные денежные средства. |
| − | PVIFA(R,n) — англ. Present Value Interest Factor of Annuity — процентный множитель современной стоимости (коэффициент приведения) аннуитета. <br> | + | PVIFA(R,n) — англ. Present Value Interest Factor of Annuity — процентный множитель современной стоимости (коэффициент приведения) аннуитета. <br> |
| − | [[Image: | + | [[Image:Tabl googl doks 12.jpg|center|Tabl googl doks 12.jpg]]PVIFA(R,n) показывает, какую сумму достаточно инвестировать в начальный момент времени, чтобы потом регулярно в течении срока, состоящего из n процентных периодов получать платежи единичного размера с учетом регулярного начисления на оставшиеся денежные средства сложных процентов по ставке R за каждый расчетный период.<br><br> |
| − | == Большое уравнение и синтаксис аннуитетных функций == | + | == Большое уравнение и синтаксис аннуитетных функций == |
| − | Производителями электронных таблиц для аннуитетных финансовых функций и их исходных аргументов были зарезервированы такие стандартные идентификаторы: | + | Производителями электронных таблиц для аннуитетных финансовых функций и их исходных аргументов были зарезервированы такие стандартные идентификаторы: |
| − | RATE (от англ. interest Rate) — процентная ставка за один период, соответствует R в общепринятой нотации; | + | RATE (от англ. interest Rate) — процентная ставка за один период, соответствует R в общепринятой нотации; |
| − | NPER (от англ. Number of PERiods) — срок (измерен числом процентных периодов) соответствует n в общепринятой нотации; | + | NPER (от англ. Number of PERiods) — срок (измерен числом процентных периодов) соответствует n в общепринятой нотации; |
| − | PMT (от англ. PayMenT) — размер платежа (член аннуитета), соответствует A в общепринятой нотации; | + | PMT (от англ. PayMenT) — размер платежа (член аннуитета), соответствует A в общепринятой нотации; |
| − | PV (от англ. Present Value) — современная стоимость; | + | PV (от англ. Present Value) — современная стоимость; |
| − | FV (от англ. Future Value) — будущая стоимость; | + | FV (от англ. Future Value) — будущая стоимость; |
| − | type — тип потока платежей (по умолчанию 0 — постнумерандо, 1 — пренумерандо). | + | type — тип потока платежей (по умолчанию 0 — постнумерандо, 1 — пренумерандо). |
| − | Для расчета неизвестных параметров аннуитета по набору известных используется большое уравнение (неявное соотношение): <br> | + | Для расчета неизвестных параметров аннуитета по набору известных используется большое уравнение (неявное соотношение): <br> |
| − | [[Image: | + | [[Image:Tabl googl doks 13.jpg]]<br> |
| − | Разрешимость этого большого уравнения обеспечивается использованием противоположных знаков перед значениями исходных данных о суммах прихода (знак +) и расхода средств (знак -). | + | Разрешимость этого большого уравнения обеспечивается использованием противоположных знаков перед значениями исходных данных о суммах прихода (знак +) и расхода средств (знак -). |
| − | Левая часть неявного соотношения собрана из трех слагаемых: расчет будущей стоимости наращением единственной начальной суммы PV по формуле сложных процентов, расчет будущей стоимости наращением аннуитета PMT (с учетом типа), будущая стоимость. | + | Левая часть неявного соотношения собрана из трех слагаемых: расчет будущей стоимости наращением единственной начальной суммы PV по формуле сложных процентов, расчет будущей стоимости наращением аннуитета PMT (с учетом типа), будущая стоимость. |
| − | При такой форме организации вычислений нулевые значения неизвестных параметров играют роль триггеров (обнуляется лишнее по контексту слагаемое). Например, указав аргумент PMT=0, пользователь получит расчет по финансовому обязательству без промежуточных платежей.<br><br> | + | При такой форме организации вычислений нулевые значения неизвестных параметров играют роль триггеров (обнуляется лишнее по контексту слагаемое). Например, указав аргумент PMT=0, пользователь получит расчет по финансовому обязательству без промежуточных платежей.<br><br> |
| − | == Использование функции FV(RATE; NPER; PMT; PV; type) == | + | == Использование функции FV(RATE; NPER; PMT; PV; type) == |
| − | <u>Пример 3</u>. Для расчета будущей стоимости вклада объемом 3 млн.руб. на 4 года по ставке 8% годовых вводим в свободную ячейку формулу, содержащую обращение ко встроенной функции =FV(0.08;4;0;-3). Ответ: +4 млн.081тыс.466руб.88 коп. | + | <u>Пример 3</u>. Для расчета будущей стоимости вклада объемом 3 млн.руб. на 4 года по ставке 8% годовых вводим в свободную ячейку формулу, содержащую обращение ко встроенной функции =FV(0.08;4;0;-3). Ответ: +4 млн.081тыс.466руб.88 коп. |
| − | <u>Пример 4</u>. Чтобы найти будущую стоимость потока 888 ежемесячных платежей по 65 долларов по номинальной годовой ставке 6% вводим формулу =FV(0.06/12;888;-65). Ответ: +1 млн.076тыс.494долл.03цента. | + | <u>Пример 4</u>. Чтобы найти будущую стоимость потока 888 ежемесячных платежей по 65 долларов по номинальной годовой ставке 6% вводим формулу =FV(0.06/12;888;-65). Ответ: +1 млн.076тыс.494долл.03цента. |
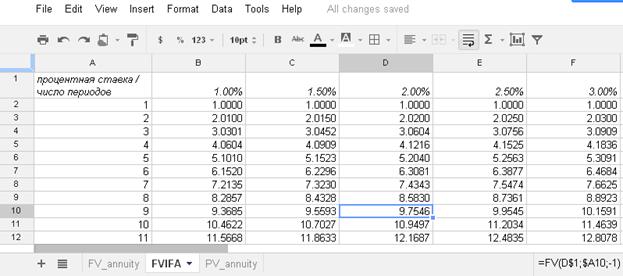
| − | Для определения коэффициента наращения срочного аннуитета из 9 единичных платежей по ставке 2% можно использовать формулу =FV(0.02;9;-1), результат 9.7546. <br> | + | Для определения коэффициента наращения срочного аннуитета из 9 единичных платежей по ставке 2% можно использовать формулу =FV(0.02;9;-1), результат 9.7546. <br> |
| − | [[Image: | + | [[Image:Tabl googl doks 14.jpg]]<br> |
| − | ''<br> | + | ''<br>Рис. 5. Таблица финансовых коэффициентов FVIFA(ставка; NPER).'' <br> |
| − | <br> | ||
| − | |||
| − | |||
| − | + | Образец построения справочной таблицы значений коэффициента FVIFA с двумя входными параметрами — процентная ставка и число периодов дан на рис.5. Знаки $ в составе адресов в формуле =FV(D$1;$A10;-1) превращают ссылки на влияющие ячейки в абсолютные (такие ссылки при копировании не сдвигаются). В данном случае значения процентных ставок для таблицы берутся из первой строки, а срок — из колонки А.<br><br> | |
| − | + | == Использование функции PV(RATE;NPER;PMT;FV;type) == | |
| − | + | <u>Пример 5</u> (вариант примера 4).Чтобы найти современную стоимость потока 888 ежемесячных платежей по 65 долларов по номинальной годовой ставке 6% вставляем в свободную ячейку табличную формулу с обращением ко встроенной функции =PV(0.06/12;888;-65). Ответ: +12тыс.844долл.95центов. Можно проверить умножением на коэффициент наращения 1,005^888. | |
| − | + | <u>Пример 6</u>. Для расчета современной стоимости вклада, дорастающего в будущем до 100 рублей за 10 месяцев по ставке 48% годовых вводим в свободную ячейку формулу, содержащую обращение ко встроенной функции =PV(0.48/12;10;0;-100). Это задача без промежуточных платежей. Ответ: +67руб.56 коп (см.ниже рис.6). <br> | |
| − | <br> | ||
| − | + | [[Image:Tabl googl doks 15.jpg]]<br> | |
| − | + | ''Рис. 6. Таблица финансовых коэффициентов PVIF(ставка; NPER).'' <br> | |
| − | |||
| − | |||
| − | + | Образец построения справочной таблицы значений коэффициента PVIFA с двумя входными параметрами — процентная ставка и срок аннуитета также представлен на рис.6. | |
| − | <u>Пример | + | <u>Пример 7</u>. Чтобы найти текущую стоимость потока 10 ежемесячных платежей по 10 рублей при годовой ставке 48%, введите =PV(0.48/12;10;-10). Ответ: +81 руб.11коп. <br> |
| − | + | [[Image:Tabl googl doks 16.jpg]]<br> | |
| − | + | ''Рис. 7. План погашения кредита десятью платежами по десять рублей.''<br> | |
| − | + | == <br>Использование функции PMT(RATE;NPER;PV;FV;type) == | |
| − | < | + | <u>Пример 8</u>. Для определения размера периодического платежа в случае погашения долга (амортизации кредита) размером 81руб.11коп. по схеме аннуитета при ставке 4% на остаток долга за период между платежами, введите =PMT(0.04;10;-81.11). Ответ: +10р. |
| − | + | При этом все платежи имеют постоянную величину, но состоят из двух неравных частей: проценты на остаток долга и погашение основного долга. Внутренняя пропорция между частями платежа изменяется: в начале срока на процентную часть приходится заметная сумма, но по мере выплаты долга (так как по «правилу США» снижается база начисления процентов) она уменьшается в пользу части, идущей в зачет погашения основного долга (см.рис.8). <br> | |
| − | + | [[Image:Tabl googl doks 17.jpg]]<br> | |
| − | + | ''Рис. 8. Динамика пропорции между частями платежа.'' | |
| − | + | <br> | |
| − | Для | + | Для определения величины этих частей аннуитетного платежа в зависимости от его порядкового номера в ряду выплат (period — номер процентного периода, он же номер платежа) запрограммированы две встроенные функции: |
| − | + | IPMT(RATE;period;NPER;PV;FV;type) — процентная часть периодического платежа; | |
| − | + | PPMT(RATE; period; NPER;PV;FV;type) — часть платежа, погашающая долг. | |
| − | + | Так, для примера 7 в первом платеже =IPMT(0.04;1;10;-81.11)=3.24р.(=0.04*81.11), а остаток долга (база новых процентов) после внесения первого платежа снизится на =PPMT(0.04;1;10;-81.11)=6.76р. Проверка: 3.24р.+ 6.76р.=10.00р. | |
| − | = | + | Для любого периода period от 1 до NPER верно PMT=IPMT(period) + PPMT(period).<br><br> |
| − | + | == Использование функции NPER(RATE;PMT;PV;FV;type) == | |
| − | <u>Пример | + | <u>Пример 9</u>. Найти срок удвоения стоимости банковского вклада по ставке 5% годовых. Вводим =NPER(0,05;0;;-1;2). В качестве пары последних аргументов в данном случае можно взять любые два числа с противоположными знаками, первое из которых вдвое меньше второго по модулю. Ответ: 14.2 года. Проверка: 1,05^14=2. |
| − | <u>Пример | + | <u>Пример 10</u>. Молодой человек c пятнадцатилетнего возраста в конце каждого месяца регулярно вносит по 15р. на сберегательный счет в банк, начисляющий на каждый платеж сложные проценты по номинальной ставке 15% годовых. В каком возрасте этот человек сможет стать миллионером (при гладком ходе событий, приводящих к результату)? Используем =NPER(0,15/12;-15;;1000000)=541.49, в месяцах. Ответ: 15+542/12=60 лет.<br><br> |
| − | + | == Использование функции RATE(NPER;PMT;PV;FV;type;guess) == | |
| − | + | В общем случае не существует явного аналитического выражения для решения аннуитетной формулы (многочлен произвольной степени NPER) относительно RATE, поэтому процентная ставка оценивается итеративно. Электронные таблицы и финансовые калькуляторы используют численный алгоритм подбора корня неявного уравнения, так что «расчет» ставки аннуитета для пользователя происходит быстро, как по точной формуле. По умолчанию последний необязательный аргумент guess равен 10%, он используется как начальное предположение на входе встроенного алгоритма подбора. | |
| − | + | <u>Пример 11</u>. При какой процентной ставке банковский вклад удвоится за три года? Применим формулу без промежуточных выплат =RATE(3;0;-1;2). Ответ: 26% годовых. | |
| − | + | <u>Пример 12</u>. При какой процентной ставке молодой человек (пример 10) станет миллионером к 50 годам? Используем формулу =RATE(25*12;-15;;100000). Ответ: 1.56% в месяц, то есть почти 19% годовых. | |
| + | <u>Пример 13</u>. Кредит на сумму 800 тыс.руб. погашается 15 платежами по 75 тыс.руб. Какова доходность банка? Введем =RATE(15;-75;800). Ответ: 4.6% за расчетный период. <br> | ||
| + | <u>Задание для самостоятельной работы</u>. Составьте план погашения кредита (см. рис.7) в электронных таблицах с помощью:<br> | ||
| − | + | а) арифметических расчетов; <br> | |
| − | + | б) финансовых функций. <br> | |
| + | <br> | ||
| + | '''''Данная публикация размещена в «Энциклопедии менеджера E-xecutive.ru» в рамках сотрудничества с проектом www.cfin.ru''''' | ||
| + | |||
| + | '''''На портале www.cfin.ru она расположена [http://www.cfin.ru/finanalysis/math/agd.shtml здесь]'''''<br> | ||
[[Category:Финансы]] | [[Category:Финансы]] | ||
Версия 19:59, 5 августа 2012
Несмотря на то, что формула сложных процентов доступна пониманию ученика средней школы, усвоившего закон геометрической прогрессии, практика потребительского кредитования подтверждает необходимость дальнейшего укрепления финансовой грамотности заемщиков.Модель процентного роста и методы оценки потоков платежей давно запрограммированы на финансовых калькуляторах и в электронных таблицах как встроенные функции.
Их имена: PV, FV, PMT стандартны - как SIN или COS для тригонометрии.
С появлением электронных таблиц воплощено в жизнь наше интуитивное восприятие компьютера как большого калькулятора. Теперь эти программы есть и на смартфонах, так что мы можем отправляться в деловой поход, вооружившись портативным вычислительным устройством.
Доступность Интернета и развитие распределенных облачных вычислений расширяет функционал наших маленьких компьютеров.
Читателю предлагается элементарный справочный материал по аннуитетным расчетам с использованием финансовых функций облачного сервиса Таблицы Google Docs.
Ранее было опубликовано пособие по технике финансовых вычислений на MS Excel, дающее ключ к применению стандартных финансовых функций, поспешно локализованных с кириллическими идентификаторами.
Содержание
- 1 Определение аннуитета
- 2 Будущая стоимость аннуитета
- 3 Современная стоимость аннуитета
- 4 Процентные множители (финансовые коэффициенты в общепринятой нотации)
- 5 Большое уравнение и синтаксис аннуитетных функций
- 6 Использование функции FV(RATE; NPER; PMT; PV; type)
- 7 Использование функции PV(RATE;NPER;PMT;FV;type)
- 8 Использование функции PMT(RATE;NPER;PV;FV;type)
- 9 Использование функции NPER(RATE;PMT;PV;FV;type)
- 10 Использование функции RATE(NPER;PMT;PV;FV;type;guess)
Определение аннуитета
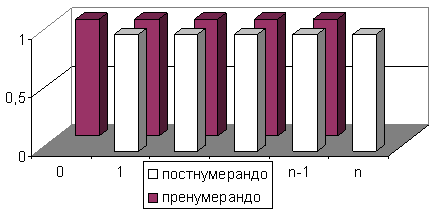
Аннуитетом называется последовательность платежей одинакового размера, поступающих через равные промежутки времени (равномерная рента). Период времени между двумя соседними платежами является расчетным для начисления процентов за использование заемных средств.
Рис. 2. Тип аннуитета задает распределение платежей по границам процентных периодов.
Конечная последовательность платежей одинакового размера называется срочным аннуитетом. Срок n соответствует количеству платежей. В зависимости от момента поступления первого платежа различают два типа аннуитетов — пренумерандо (первый платеж поступает в начале первого периода) и постнумерандо (первый платеж поступает в конце первого периода). Аннуитет постнумерандо называют «обыкновенным».
Будущая стоимость аннуитета
Будущая стоимость (FV — англ. Future Value) равномерного потока платежей с учетом ставки процента за каждый период между платежами находится как сумма геометрической прогрессии
где A — член аннуитета (размер одного платежа), R — процентная ставка, n — число платежей (и число процентных периодов).
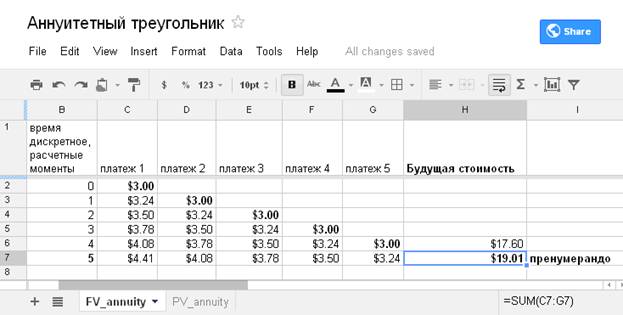
Пример 1. Согласно условиям договора, 5 платежей по 3 доллара регулярно приходят по схеме пренумерандо. Получатель аннуитета (кредитор) использует средства с доходностью R = 8% за период между платежами. Будущая стоимость одного платежа A=$3.00 через 1 расчетный период по ставке 8% составляет $3.00*1.08=$3.24. Через 2 периода по формуле сложных процентов $3.00*1.08*1.08=$3.24*1.08=$3.50. Какова будущая стоимость всего потока платежей в конце последнего периода? Детальный расчет будущей стоимости каждого платежа и всего аннуитета развернут на рис. 2.
Рис. 3. Вычисление будущей стоимости аннуитета по частям.
Ответ: В условиях примера 1 поток платежей пренумерандо позволяет их получателю накопить сумму $19.01. В случае аннуитета постумерандо будущая стоимость достигает только $17.60 (все платежи «недорасли» бы еще один период).
Современная стоимость аннуитета
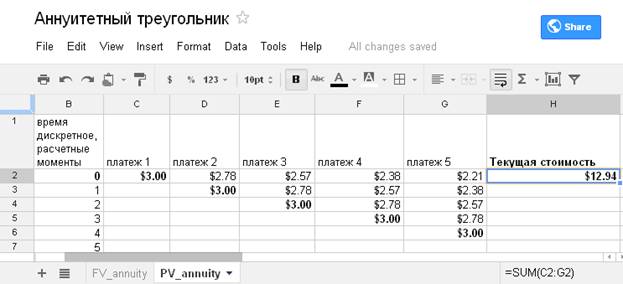
Пример 2. Расчет современной (текущей, приведенной, дисконтированной) стоимости каждого из пяти периодических платежей и всего потока по ставке R=8% за период между платежами для аннуитета пренумерандо представлен в таблице на рис. 4 в варианте приведения дисконтирующими множителями к начальному моменту времени (отсчет ведется от 0), когда вносится первый платеж.
Ответ: Текущая стоимость данного аннуитета равна $12.94.
Рис. 4. Вычисление современной (текущей) стоимости аннуитета по частям.
Современная стоимость (PV — англ. Present Value) срочного аннуитета (n < ∞) аналически оценивается как разница современных стоимостей двух бесконечных аннуитетов, моменты начала которых не совпадают.
Здесь использован результат из элементарной алгебры — современная стоимость бесконечного аннуитета PV (n = +∞) представляет собой сумму всех членов бесконечно убывающей геометрической прогрессии со знаменателем 1/(1+R), которая при R < –2 или R > 0 сходится к A/R:
Для вывода рабочей формулы современной стоимости срочного аннуитета из современной стоимости вечной ренты на момент времени 0 вычитается современная стоимость ее клона — вечной ренты, начинающейся на n периодов попозже.
Вторая стоимость численно равна первой, но относится к моменту времени n, поэтому перед вычитанием ее необходимо дисконтировать по той же процентной ставке R на n расчетных периодов в прошлое. Эквивалентная будущая стоимость срочного аннуитета есть.
В рассмотренном выше примере 1 верно $19.01=$12.94*1.08^5=$3.00*FVIFA(8%,5).
Процентные множители (финансовые коэффициенты в общепринятой нотации)
FVIF(R,n) — англ. Future Value Interest Factor - процентный множитель будущей стоимости (коэффициент наращения).
FVIF(R,n) показывает, какую сумму можно нарастить из одной исходной денежной единицы благодаря регулярному присоединению сложных процентов по ставке R в течение n процентных периодов (срок наращения).
PVIF(R,n) — англ. Present Value Interest Factor — процентный множитель современной стоимости (коэффициент приведения).
FVIFA(R,n) — англ. Future Value Interest Factor of Annuity — процентный множитель будущей стоимости (коэффициент наращения) аннуитета.
PVIFA(R,n) — англ. Present Value Interest Factor of Annuity — процентный множитель современной стоимости (коэффициент приведения) аннуитета.
Большое уравнение и синтаксис аннуитетных функций
Производителями электронных таблиц для аннуитетных финансовых функций и их исходных аргументов были зарезервированы такие стандартные идентификаторы:
RATE (от англ. interest Rate) — процентная ставка за один период, соответствует R в общепринятой нотации;
NPER (от англ. Number of PERiods) — срок (измерен числом процентных периодов) соответствует n в общепринятой нотации;
PMT (от англ. PayMenT) — размер платежа (член аннуитета), соответствует A в общепринятой нотации;
PV (от англ. Present Value) — современная стоимость;
FV (от англ. Future Value) — будущая стоимость;
type — тип потока платежей (по умолчанию 0 — постнумерандо, 1 — пренумерандо).
Для расчета неизвестных параметров аннуитета по набору известных используется большое уравнение (неявное соотношение):
Разрешимость этого большого уравнения обеспечивается использованием противоположных знаков перед значениями исходных данных о суммах прихода (знак +) и расхода средств (знак -).
Левая часть неявного соотношения собрана из трех слагаемых: расчет будущей стоимости наращением единственной начальной суммы PV по формуле сложных процентов, расчет будущей стоимости наращением аннуитета PMT (с учетом типа), будущая стоимость.
При такой форме организации вычислений нулевые значения неизвестных параметров играют роль триггеров (обнуляется лишнее по контексту слагаемое). Например, указав аргумент PMT=0, пользователь получит расчет по финансовому обязательству без промежуточных платежей.
Использование функции FV(RATE; NPER; PMT; PV; type)
Пример 3. Для расчета будущей стоимости вклада объемом 3 млн.руб. на 4 года по ставке 8% годовых вводим в свободную ячейку формулу, содержащую обращение ко встроенной функции =FV(0.08;4;0;-3). Ответ: +4 млн.081тыс.466руб.88 коп.
Пример 4. Чтобы найти будущую стоимость потока 888 ежемесячных платежей по 65 долларов по номинальной годовой ставке 6% вводим формулу =FV(0.06/12;888;-65). Ответ: +1 млн.076тыс.494долл.03цента.
Для определения коэффициента наращения срочного аннуитета из 9 единичных платежей по ставке 2% можно использовать формулу =FV(0.02;9;-1), результат 9.7546.
Рис. 5. Таблица финансовых коэффициентов FVIFA(ставка; NPER).
Образец построения справочной таблицы значений коэффициента FVIFA с двумя входными параметрами — процентная ставка и число периодов дан на рис.5. Знаки $ в составе адресов в формуле =FV(D$1;$A10;-1) превращают ссылки на влияющие ячейки в абсолютные (такие ссылки при копировании не сдвигаются). В данном случае значения процентных ставок для таблицы берутся из первой строки, а срок — из колонки А.
Использование функции PV(RATE;NPER;PMT;FV;type)
Пример 5 (вариант примера 4).Чтобы найти современную стоимость потока 888 ежемесячных платежей по 65 долларов по номинальной годовой ставке 6% вставляем в свободную ячейку табличную формулу с обращением ко встроенной функции =PV(0.06/12;888;-65). Ответ: +12тыс.844долл.95центов. Можно проверить умножением на коэффициент наращения 1,005^888.
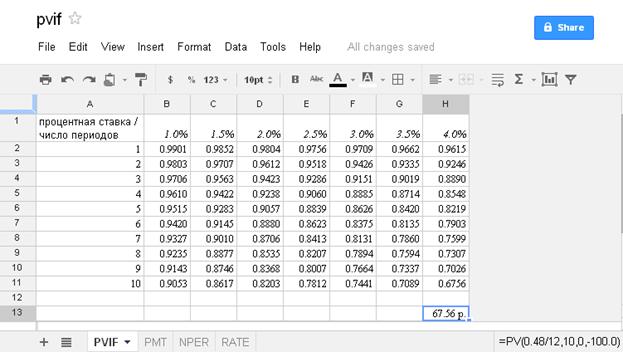
Пример 6. Для расчета современной стоимости вклада, дорастающего в будущем до 100 рублей за 10 месяцев по ставке 48% годовых вводим в свободную ячейку формулу, содержащую обращение ко встроенной функции =PV(0.48/12;10;0;-100). Это задача без промежуточных платежей. Ответ: +67руб.56 коп (см.ниже рис.6).
Рис. 6. Таблица финансовых коэффициентов PVIF(ставка; NPER).
Образец построения справочной таблицы значений коэффициента PVIFA с двумя входными параметрами — процентная ставка и срок аннуитета также представлен на рис.6.
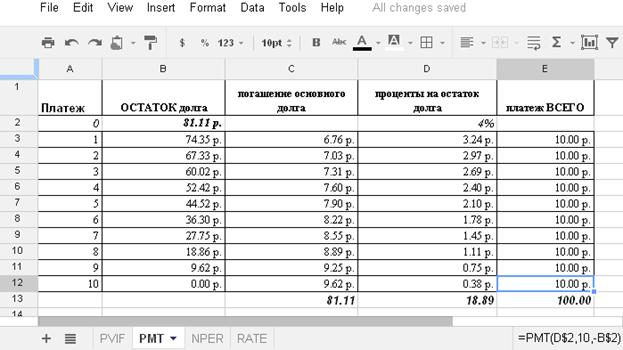
Пример 7. Чтобы найти текущую стоимость потока 10 ежемесячных платежей по 10 рублей при годовой ставке 48%, введите =PV(0.48/12;10;-10). Ответ: +81 руб.11коп.
Рис. 7. План погашения кредита десятью платежами по десять рублей.
Использование функции PMT(RATE;NPER;PV;FV;type)
Пример 8. Для определения размера периодического платежа в случае погашения долга (амортизации кредита) размером 81руб.11коп. по схеме аннуитета при ставке 4% на остаток долга за период между платежами, введите =PMT(0.04;10;-81.11). Ответ: +10р.
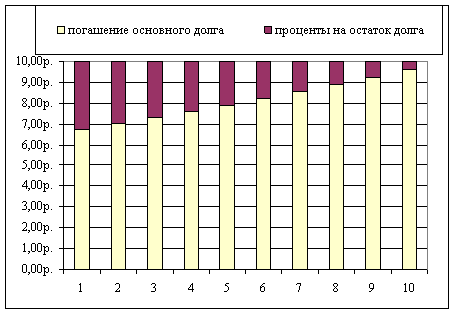
При этом все платежи имеют постоянную величину, но состоят из двух неравных частей: проценты на остаток долга и погашение основного долга. Внутренняя пропорция между частями платежа изменяется: в начале срока на процентную часть приходится заметная сумма, но по мере выплаты долга (так как по «правилу США» снижается база начисления процентов) она уменьшается в пользу части, идущей в зачет погашения основного долга (см.рис.8).
Рис. 8. Динамика пропорции между частями платежа.
Для определения величины этих частей аннуитетного платежа в зависимости от его порядкового номера в ряду выплат (period — номер процентного периода, он же номер платежа) запрограммированы две встроенные функции:
IPMT(RATE;period;NPER;PV;FV;type) — процентная часть периодического платежа;
PPMT(RATE; period; NPER;PV;FV;type) — часть платежа, погашающая долг.
Так, для примера 7 в первом платеже =IPMT(0.04;1;10;-81.11)=3.24р.(=0.04*81.11), а остаток долга (база новых процентов) после внесения первого платежа снизится на =PPMT(0.04;1;10;-81.11)=6.76р. Проверка: 3.24р.+ 6.76р.=10.00р.
Для любого периода period от 1 до NPER верно PMT=IPMT(period) + PPMT(period).
Использование функции NPER(RATE;PMT;PV;FV;type)
Пример 9. Найти срок удвоения стоимости банковского вклада по ставке 5% годовых. Вводим =NPER(0,05;0;;-1;2). В качестве пары последних аргументов в данном случае можно взять любые два числа с противоположными знаками, первое из которых вдвое меньше второго по модулю. Ответ: 14.2 года. Проверка: 1,05^14=2.
Пример 10. Молодой человек c пятнадцатилетнего возраста в конце каждого месяца регулярно вносит по 15р. на сберегательный счет в банк, начисляющий на каждый платеж сложные проценты по номинальной ставке 15% годовых. В каком возрасте этот человек сможет стать миллионером (при гладком ходе событий, приводящих к результату)? Используем =NPER(0,15/12;-15;;1000000)=541.49, в месяцах. Ответ: 15+542/12=60 лет.
Использование функции RATE(NPER;PMT;PV;FV;type;guess)
В общем случае не существует явного аналитического выражения для решения аннуитетной формулы (многочлен произвольной степени NPER) относительно RATE, поэтому процентная ставка оценивается итеративно. Электронные таблицы и финансовые калькуляторы используют численный алгоритм подбора корня неявного уравнения, так что «расчет» ставки аннуитета для пользователя происходит быстро, как по точной формуле. По умолчанию последний необязательный аргумент guess равен 10%, он используется как начальное предположение на входе встроенного алгоритма подбора.
Пример 11. При какой процентной ставке банковский вклад удвоится за три года? Применим формулу без промежуточных выплат =RATE(3;0;-1;2). Ответ: 26% годовых.
Пример 12. При какой процентной ставке молодой человек (пример 10) станет миллионером к 50 годам? Используем формулу =RATE(25*12;-15;;100000). Ответ: 1.56% в месяц, то есть почти 19% годовых.
Пример 13. Кредит на сумму 800 тыс.руб. погашается 15 платежами по 75 тыс.руб. Какова доходность банка? Введем =RATE(15;-75;800). Ответ: 4.6% за расчетный период.
Задание для самостоятельной работы. Составьте план погашения кредита (см. рис.7) в электронных таблицах с помощью:
а) арифметических расчетов;
б) финансовых функций.
Данная публикация размещена в «Энциклопедии менеджера E-xecutive.ru» в рамках сотрудничества с проектом www.cfin.ru
На портале www.cfin.ru она расположена здесь